The Road to Q-Day

For decades, the security of the modern digital world has rested upon the mathematical complexity of prime factorization. RSA (Rivest–Shamir–Adleman) and Elliptic Curve Cryptography (ECC) are the silent guardians of everything from secure web browsing to global financial transactions. However, the emergence of quantum computing and specifically Shor’s Algorithm has placed a definitive “expiration date” on these classical cryptographic standards.

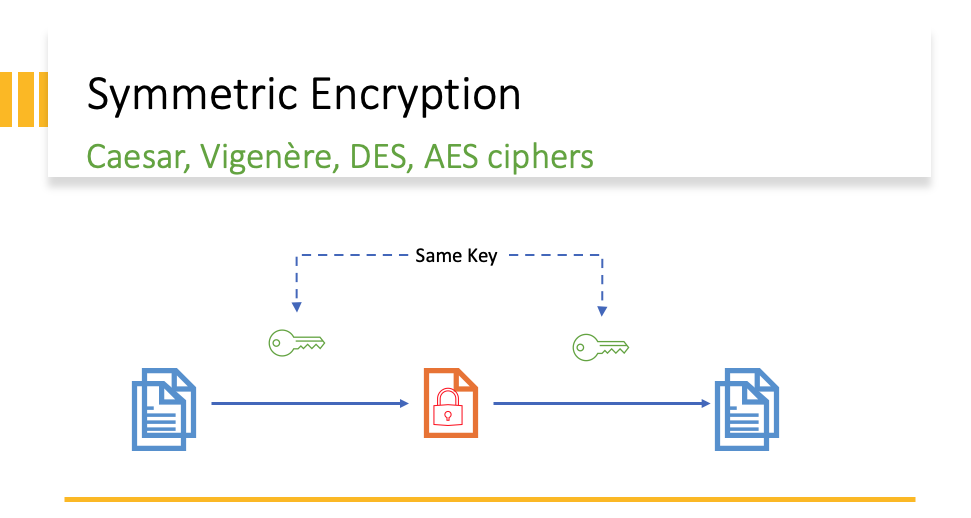
The Bedrock of Modern Security: RSA Cryptography

RSA is an asymmetric encryption system that relies on a public key for encryption and a private key for decryption. The security of this system is derived from the “factoring problem” – the observation that while it is computationally trivial to multiply two large prime numbers ( $p$ and $q$ ) to get a product ( $n$ ), it is nearly impossible for a classical computer to do the reverse for very large numbers.

The Mathematical Foundation

The process of generating RSA keys involves several critical steps:

Selecting Primes: Two large prime numbers, $p$ and $q$ , are chosen to compute $n = p \times q$ .
Euler’s Totient: The value $\phi(n) = (p-1) \times (q-1)$ is calculated.
The Public Exponent: An integer $e$ is chosen such that it is relatively prime to $\phi(n)$ (commonly 65,537).
The Private Key: The decrypter $d$ is calculated as the modular inverse of $e$ such that $(d \times e) \mod \phi(n) = 1$ .

The public key $(e, n)$ can be shared openly, while the private key $(d, n)$ remains secret. As long as $p$ and $q$ remain hidden, the private key $d$ cannot be derived from the public information.

Sample Key Generation

import math

def generate_keys(p, q):
    n = p * q
    phi = (p - 1) * (q - 1)

    # Choose e such that 1 < e < phi and gcd(e, phi) = 1
    # 65537 is the standard choice for e
    e = 65537
    if math.gcd(e, phi) != 1:
          e = 3 # Fallback for small primes

# Compute d (the modular multiplicative inverse of e mod phi)
d = pow(e, -1, phi)

return ((e, n), (d, n))

# Example usage with small primes
p, q = 61, 53
public_key, private_key = generate_keys(p, q)

print(f"Public Key (e, n): {public_key}")
print(f"Private Key (d, n): {private_key}")

4 bit numbers

p, q = 11, 13
Public Key (e, n): (65537, 143)
Private Key (d, n): (113, 143)

8 bit numbers

p, q = 149, 239
Public Key (e, n): (65537, 35611)
Private Key (d, n): (22041, 35611)

16 bit numbers

p, q = 37897, 37747
Public Key (e, n): (65537, 1430498059)
Private Key (d, n): (77832161, 1430498059)

24 bit numbers

p, q = 9787039, 8448197
Public Key (e, n): (65537, 82682833518683)
Private Key (d, n): (68460568664129, 82682833518683)

Encryption / Decryption

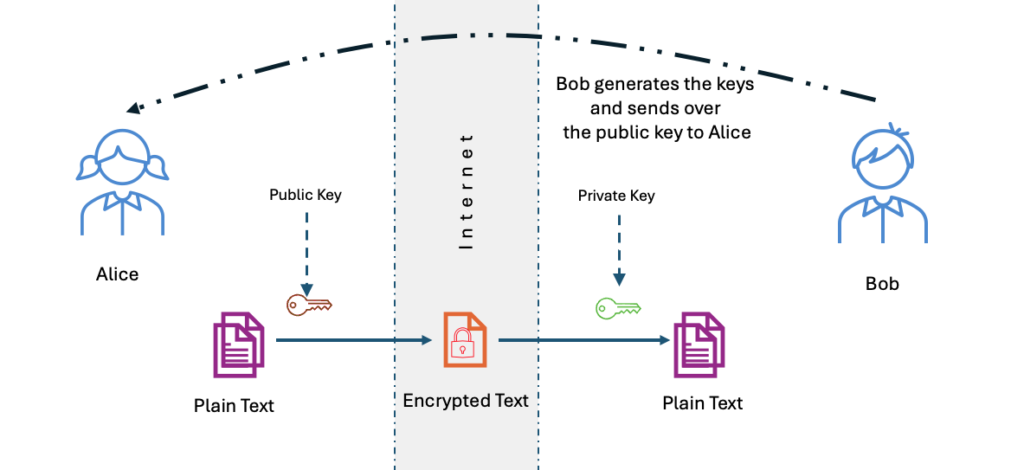
import math

def encrypt(public_key, plaintext):
    e, n = public_key
    # Convert string to list of integers (ASCII)
    cipher = [pow(ord(char), e, n) for char in plaintext]
    return cipher

def decrypt(private_key, ciphertext):
    d, n = private_key
    # Convert integers back to characters
    plain = "".join([chr(pow(char, d, n)) for char in ciphertext])
    return plain

# Test the implementation
message = "Hello from PQCrypto"
encrypted_msg = encrypt(public_key, message)
decrypted_msg = decrypt(private_key, encrypted_msg)

print(f"Original: {message}")
print(f"Encrypted: {encrypted_msg}")
print(f"Decrypted: {decrypted_msg}")

4 bit numbers

p, q = 11, 13
Public Key (e, n): (65537, 143)
Private Key (d, n): (113, 143)
message = "Hello from PQCrypto"
encrypted_msg = encrypt(public_key, message)
decrypted_msg = decrypt(private_key, encrypted_msg)
Encrypted:[63, 95, 114, 114, 89, 54, 20, 82, 89, 109, 54, 97, 126,  45, 82, 88, 73, 129, 89]
Decrypted: Hello from PQCrypto

8 bit numbers

p, q = 149, 239
Public Key (e, n): (65537, 35611)
Private Key (d, n): (22041, 35611)
message = "Hello from PQCrypto"
encrypted_msg = encrypt(public_key, message)
decrypted_msg = decrypt(private_key, encrypted_msg)
Encrypted: [27575, 19283, 29510, 29510, 11101, 1636, 24469, 4119, 11101, 33730, 1636, 775, 28008, 27433, 4119, 18545, 24462, 6578, 11101]
Decrypted: Hello from PQCrypto

16 bit numbers

p, q = 37897, 37747
Public Key (e, n): (65537, 1430498059)
Private Key (d, n): (77832161, 1430498059)
message = "Hello from PQCrypto"
encrypted_msg = encrypt(public_key, message)
decrypted_msg = decrypt(private_key, encrypted_msg)
Encrypted: [636432436, 1129508596, 388858209, 388858209, 428719780, 1169212451, 1116860776, 646535258, 428719780, 1072491772, 1169212451, 23553126, 995586588, 41065687, 646535258, 836884807, 360713278, 1252818906, 428719780]
Decrypted: Hello from PQCrypto

24 bit numbers

p, q = 9787039, 8448197
Public Key (e, n): (65537, 82682833518683)
Private Key (d, n): (68460568664129, 82682833518683)
message = "Hello from PQCrypto"
encrypted_msg = encrypt(public_key, message)
decrypted_msg = decrypt(private_key, encrypted_msg)
Encrypted: [56142991463916, 76291152739381, 75073620225918, 75073620225918, 16380971877665, 64403795058036, 25024513605508, 78280700355632, 16380971877665, 24606989774293, 64403795058036, 9300671480964, 344302026804, 81161641420759, 78280700355632, 54801574199622, 11023238551839, 48174395344901, 16380971877665]
Decrypted: Hello from PQCrypto

Breaking the key - Brute force

import math

def get_private_key(public_key):
    e, n = public_key
    # 1. Factor n to find p and q (Classical Trial Division)
    p, q = None, None
    for i in range(2, int(math.sqrt(n)) + 1):
        if n % i == 0:
            p = i
            q = n // i
            break
        if not p:
            return "Failed to factor n. It might be prime or too large."

    print(f"Factors found: p = {p}, q = {q}")

    # 2. Calculate Euler's Totient: phi(n) = (p-1)(q-1)
    phi = (p - 1) * (q - 1)

    # 3. Calculate d (modular inverse of e mod phi)
    # pow(base, -1, mod) is the Pythonic way to find the modular inverse
    try:
        d = pow(e, -1, phi)
        return (d, n)
    except ValueError:
        return "e is not invertible mod phi. Public key is invalid."

4 bit numbers

p, q = 11, 13
public_key = (65537, 35611)
private_key = get_private_key(public_key)
Factors found: p = 11, q = 13
Public Key: (65537, 143)
Private Key d: (113, 143)

8 bit numbers

p, q = 149, 239
public_key = (65537, 35611)
private_key = get_private_key(public_key)
Factors found: p = 149, q = 239
Public Key: (65537, 35611)
Private Key: (22041, 35611)

16 bit numbers

p, q = 37897, 37747
public_key = (65537, 1430498059)
private_key = get_private_key(public_key)
Factors found: p = 37747, q = 37897
Public Key: (65537, 1430498059)
Private Key: (77832161, 1430498059)

24 bit numbers

p, q = 8448197, 9787039
public_key = (65537, 82682833518683)
private_key = get_private_key(public_key)
Factors found: p = 8448197, q = 9787039
Public Key: (65537, 82682833518683)
Private Key: (68460568664129, 82682833518683)

Example of a real key RSA-2048

So far we played with small sized keys, lets see what a real RSA-2048 key size looks like

!pip install cryptography

from cryptography.hazmat.primitives.asymmetric import rsa

# Generate 2048-bit RSA key
key = rsa.generate_private_key(
    public_exponent=65537,
    key_size=2048
)

numbers = key.private_numbers()

n = numbers.public_numbers.n
e = numbers.public_numbers.e
d = numbers.d
p = numbers.p
q = numbers.q

print("n =", n)
print("e =", e)
print("d =", d)
print("p =", p)
print("q =", q)

Prime p: (309 digits) 
142634142859514559478783335047596216854570265610654740792801636386855014783921741183797661600754666631291909940669108636063547004655120921076200277965385860485156252950209224403433752761271863306775605723451166070967923331763161133914297441314314455871498896626145608896683338765047186915151292763078401175359

Prime q: (309 digits) 
135325839987359134454763468272433120910194798073121989766882092352948840665999724725665386386997212306000883277391415878708086612827548741640130611710219965417148515882625552450781880286704862017111233130052766305074970929826780430390856027171787909384058118439531485045740922703498099252628576990266046829071

Public Exponent (e): 65537

Public/Private Modulus (n = p x q): (617 digits) 
19302085193340790731649134122755610597929021482849409121517469153503374560260051130664595591104593955496760989314486636731126094519700631160572205713538784622914231219202871447486887877700031265197458525386396485949846206244415456353189321198579529754990972799363368205599219051180174559825498258824467587815597465847047767724421958712870043237096312282073581696845798440968413766672782132150021922078813339873415228750030661054624755077368789452375921661843276063311600554100745594801400894003744510821714435170661177392424555976278300697474161225874456600484957230696972084374014284268487042131021086682701370061489

Private exponent (d) = (modular inverse of e) so [ d * e mod ((p-1)(q-1)) = 1 ]: (617 digits) 
3301002042311420762627576716173228612563719315497752070341452832330833301362507485427907706869406427715758993671311873056173783776749083327703332188494174253530413407766998537977524746834031927313320950799254342043820685713221667680951918946452833811342277234772184122684224897777246387026018653354664277037919053690677992893994447726967004223319773276526434442561221503801795319971707926014681536549012265654089449584850104373692323196399036126195960959068240047925345791862348664838977255669198244348378041404438689627898830652886569863810644963071374555876087059474732658692910279316138169291179143984989126484513

Time needed - Cracking the prime factorization problem

Key Bit Size	Classical Time (GNFS/Brute Force)	Quantum Time (Shor's Algorithm)	Logical Qubits Needed
4-bit	< 1 Microsecond	Milliseconds (Simulated)	~8
8-bit	< 1 Microsecond	Milliseconds (Simulated)	~16
16-bit	< 1 Microsecond	Milliseconds (Simulated)	~32
32-bit	< 1 Millisecond	Milliseconds (Simulated)	~64
64-bit	~1-10 Milliseconds	Seconds	~128
128-bit	~1-2 Minutes	Minutes	~256
256-bit	~Weeks to Months	Minutes	~512
512-bit	~8 Months (Distributed)	Minutes	~1024
1024-bit	~2000 Years	~30 Minutes	~2048
2048-bit	~6.4 Quadrillion Years	~4-8 Hours	~4096
4096-bit	~Exceeds Age of Universe	~1-2 Days	~8192

Note: most common size used is RSA-2048

Shor's algorithm

In 1994, mathematician Peter Shor realized that while factoring is hard for classical computers, it is just a specific case of a broader problem called Order Finding (or Period Finding). If you can find the “period” of a specific mathematical function, you can find the factors of $n$ .

Let’s say we have a number N=77 for which we have to findprime factors of.

We will Guess a number g (Lets say 8) and keep multiplying 8 with itself (g^r).

Then we divide it by N(77) and find out remainders till we get a “1”

In below example 8^10 / 77 gives us a remainder 1

g^r	Result	g^r / 77	Remainder
8^1	8	0	8
8^2	64	0	64
8^3	512	6	50
8^4	4096	53	15
8^5	32708	425	43
8^6	202144	3404	36
8^7	2097152	27235	57
8^8	16777216	217885	71
8^9	134217728	1743087	29
8^10	1073741824	13944699	1

8^10 = 13944699 x 77 + 1

8^10 – 1 = 13944699 x 77

g^r – 1 = mN

( g^(r/2) – 1 ) x ( g^(r/2) + 1 ) = mN ## which is one number multiplied by another number = mN

Int1 x Int2 = mN ## And we know Int1 is a multiple of p or q and same with Int2

(A1 * p) * (A2 * q) = m(p * q)

We just need to remove A1 and A2 now

A1 * A2 = m

g = 8, r = 10

(g^5 – 1) = 32,767 = A1 * p

(g^5 + 1) = 32,769 = A2 * q

Euclid's theorem - Finding the factor

Now we repeat the division steps like below to converge on the prime factor

Shor’s algorithm – On a Quantum computer

Shor’s algorithm has existed since 1994. What is changing now is that a Quantum computer can use supoerpositioned qubits to identify the frequency of the remainders to get the distance between the repetition of remainders to get the value of “r”

Take 2 sets of qubits

|x> = |0> |1> |2> |3> . . . . . . . . |4096>

|w> =|0> |0> |0> |0> . . . . . . . . |4096>

Take random number g and raise it to the power of first set off qubits

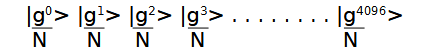
Store result in |w>

|x> and |w> are now entangled

Now we measure the remainder part of the superposition, which will give us multiple terms in our superposition results.
The frequency/distance between the results gives us the value of (r) to substitute in Eculid’s theorem

Q-Day is coming up fast

Physical vs Logical Qubits

To break a 2048-bit RSA key, a quantum computer needed approximately 20 million physical qubits.

Today’s leading quantum processors (like IBM’s Osprey or Condor) operate in the range of 433 to 1,121 physical qubits.

Physical qubits are noisy and prone to error (decoherence).

To perform reliable calculations, many physical qubits must be bundled together to create a single “logical qubit” through error correction.

Algorithm	Classical Security (Bits)	Quantum Security (Bits)	Quantum Attack Method	Logical Qubits to Break
AES-128	128	64	Grover’s	N/A (Symmetric)
AES-256	256	128	Grover’s	N/A (Symmetric)
RSA-2048	112	~0	Shor’s	~4,096
RSA-3072	128	~0	Shor’s	~6,144
ECC-256	128	~0	Shor’s	~2,330
ECC-384	192	~0	Shor’s	~3,480

Why the Deadline is Accelerating

Algorithmic Efficiency: Physical – to – Logical qubit ratio is rapidly decreasing due to breakthroughs in Quantum Error Correction (QEC). To 1000:1
Hardware Fidelity: As the fidelity of individual physical qubits improves, fewer of them are needed to maintain a stable logical qubit.
IBM intends to demonstrate error-corrected logical qubits by 2026-2029, which significantly compresses the time remaining until Q-Day.
State actors with unlimited budgets are targeting quantum breakthroughs behind closed doors.
These numbers are not static. Mathematical research continues to find “shortcuts” that lower the qubit count further, meaning the goalposts for our defense are constantly moving closer.