Quantum teleportation is a real process in quantum physics that allows the state of a particle (like an electron or photon) to be transferred from one place to another — without physically moving the particle itself. It’s not like “Star Trek”-style teleportation of objects or people, but it’s still amazing and real science.
Quantum teleportation transfers information — the quantum state of a particle — from one particle to another, at a different location.
Quantum entanglement
This is possible through Quantum entanglement which is a phenomenon where two or more particles become linked in such a way that the state of one particle immediately affects the state of the other(s) — no matter how far apart they are.
Imagine you have two coins that are perfectly connected. You flip them separately, even on opposite sides of the galaxy — but the moment one lands on heads, the other must land on tails.
That’s what entanglement is like. But instead of heads and tails, we’re talking about quantum states (like spin-up or spin-down, |0⟩ or |1⟩).
What Happens in Entanglement?
If two particles are entangled:
– They don’t have individual states until one is measured.
– Measuring one particle instantly determines the state of the other.
– This correlation is stronger than anything allowed in classical physics.
Example: Entangled Qubits
Let’s say we create an entangled pair of qubits in this state: |ψ⟩ = (1/√2)(|00⟩ + |11⟩)
This means:
– If the first qubit is measured as 0, the second will definitely be 0.
– If the first qubit is measured as 1, the second will definitely be 1.
– But before measurement, neither qubit has a definite value — they’re both in superposition, and only when one is observed does the other’s state become real too.
Quantum teleportation - The 4 steps:
Let’s say we have three particles:
A: The particle whose quantum state you want to teleport (the “message”).
B and C: A pair of particles that are entangled (created beforehand and separated — B stays with you, C goes far away).
1. Entanglement Setup
Particles B and C are entangled. This means measuring one instantly affects the other, even at great distances.
2. Measurement
You perform a special joint measurement on particles A and B. This combines their states and destroys the original state of A, but it creates a set of classical bits (regular information, like 00, 01, 10, or 11).
3. Send Classical Info
You send this classical info (2 bits) to the person who has particle C. This can’t go faster than light — it follows normal physics rules.
4. Reconstruction
The person with particle C uses the 2 bits to apply a specific operation to C, which turns it into an exact copy of what particle A was.
Notes:
- The original state is destroyed — no copying or cloning is involved (quantum no-cloning theorem).
- You need entanglement + classical communication to make it work.
- No actual faster-than-light travel happens, even though entanglement is spooky.
- Only the state, not the particle itself, is moved.
Concrete example
STEP 1
Alice has to transfer a qubit |ψ⟩ to Bob.
|ψ⟩ = α|0⟩ + β|1⟩
Charlie generates a pair of entangled qubits and gives 1 each to Alice and Bob
Entangled qubit is |ε⟩ = (1/√2)(|00⟩ + |11⟩)
Showing first one for Alice and second for Bob
|ε⟩ = (1/√2) (|0⟩(Alice)|0⟩(Bob) + |1⟩(Alice)|1⟩(Bob))
Now we have 3 qubits, The first 2 are with Alice, and 3rd one is with Bob
|ψ⟩ ⨂ |ε⟩ = (1/√2) ( α|0⟩⨂(|00⟩ + |11⟩) + β|1⟩⨂(|00⟩ + |11⟩) )
|ψ⟩ ⨂ |ε⟩ = (1/√2) ( α|000⟩ + α|011⟩ + β|100⟩ + β|111⟩ )
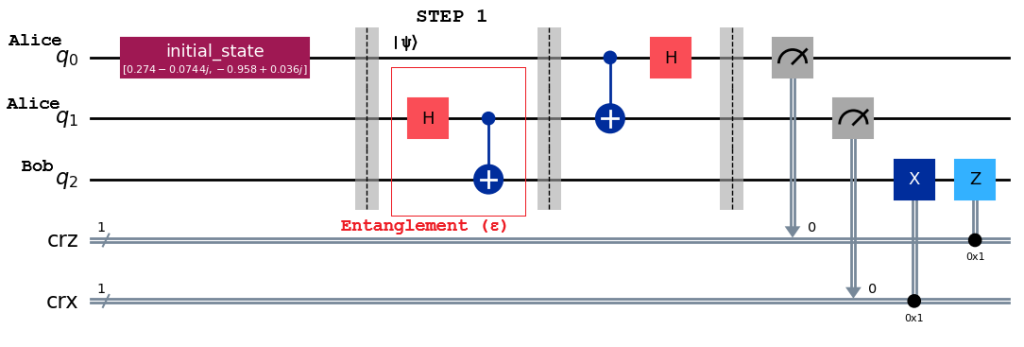
STEP 2
Alice applies CNOT gate on q0 and q1, followed by a hadamard gate on q0
( H ⨂ I ⨂ I ) ( CNOT ⨂ I ) ( |ψ⟩ ⨂ |ε⟩ )
= ( H ⨂ I ⨂ I ) ( CNOT ⨂ I ) (1/√2) ( α|000⟩ + α|011⟩ + β|100⟩ + β|111⟩ )
= ( H ⨂ I ⨂ I ) (1/√2) ( α|000⟩ + α|011⟩ + β|110⟩ + β|101⟩ )
= (1/2) ( α(|000⟩ + |011⟩ + |100⟩ + |111⟩) + β(|010⟩ + |001⟩ – |110⟩ – |101⟩) )
= (1/2) ( |00⟩(α(|0⟩ + β|1⟩) + |01⟩(α(|1⟩ + β|0⟩) + |10⟩(α(|0⟩ – β|1⟩) + |11⟩(α(|1⟩ – β|0⟩) )
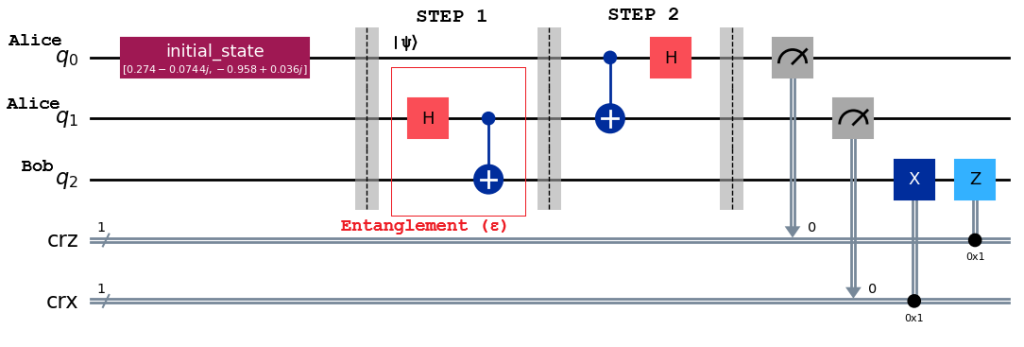
STEP 3
Alice measures first 2 qubits, and sends them as 2 classical bits to Bob.
She gets results which are one of four standard states: |00⟩, |01⟩, |10⟩, |11⟩
And Bob’s state will be
Alice Bob
|00⟩ -> α|0⟩ + β|1⟩
|01⟩ -> α|1⟩ + β|0⟩
|10⟩ -> α|0⟩ – β|1⟩
|11⟩ -> α|1⟩ – β|0⟩
So Bob will have to apply certain transformations to get the original state back from these projected states.
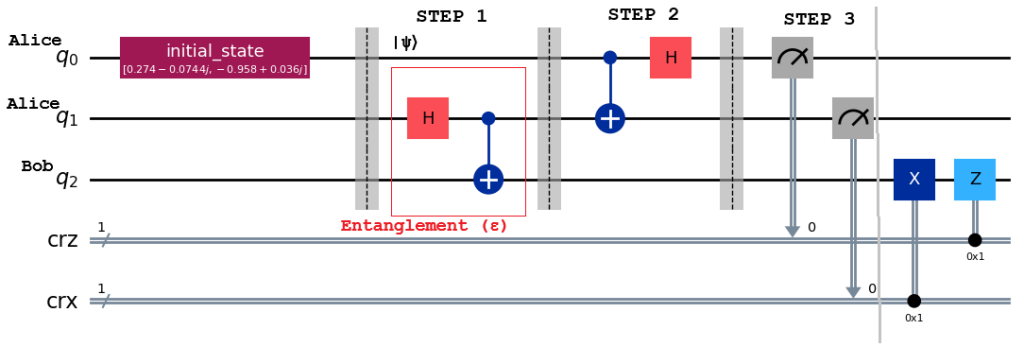
STEP 4
Bob will have to apply reverse transformations as follows
Bob Bits received Equivalent Gate
α|0⟩ + β|1⟩ 00 I
α|1⟩ + β|0⟩ 01 X
α|0⟩ – β|1⟩ 10 Z
α|1⟩ – β|0⟩ 11 ZX
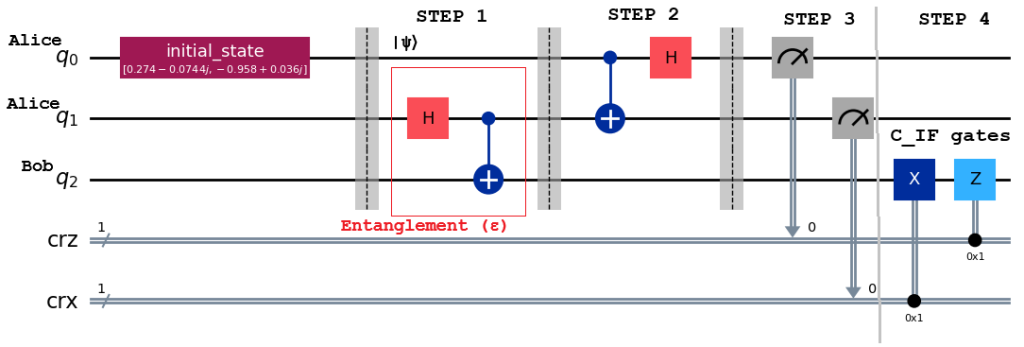
Here we apply C_IF gates based on bits received, when the bit is 1, then only the gate will be applied.
Code
This code is for google colab. Let’s install needed libraries first.
!pip install qiskit==1.2.0 ipywidgets
!pip install qiskit-aer
!pip install pylatexenc
Next we import the needed libraries
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer import Aer
from qiskit.visualization import plot_bloch_multivector, array_to_latex
from qiskit.quantum_info import random_statevector
import qiskit.quantum_info as qi
from qiskit.circuit.library import StatePreparation, Initialize
Create the qubit to be teleported
# Create random 1-qubit state
psi = random_statevector(2)
print('psi state: {}'.format(psi))
# Display it in LaTeX
array_to_latex(psi)
psi state: Statevector([ 0.27394095-0.07436968j, -0.95819034+0.03601074j], dims=(2,))
[0.2739409502−0.0743696775i−0.9581903431+0.0360107387i]
plot_bloch_multivector(psi)
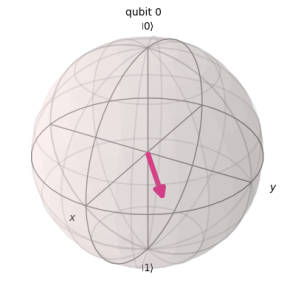
First initialize the state from ψ
init_state = Initialize(psi)
init_state.label = "initial_state"
Step 1 : Alice has to transfer a qubit |ψ⟩ to Bob.
def step1(qc, a, b):
"""Creates a bell pair in qc using qubits a & b"""
qc.h(a) # hadamard gate
qc.cx(a,b) # CNOT with a as control and b as target
Step 2: Alice applies CNOT gate on q0 and q1, followed by a hadamard gate on q0
def step2(qc, psi, a):
qc.cx(psi, a)
qc.h(psi)
Step 3: Alice measures first 2 qubits, and sends them as 2 classical bits to Bob.
def step3(qc, a, b):
"""Measures qubits a & b and 'sends' the results to Bob"""
qc.barrier()
qc.measure(a,0)
qc.measure(b,1)
Step 4: Bob will have to apply reverse transformations using c_if gates
# This function takes a QuantumCircuit (qc), integer (qubit)
# and ClassicalRegisters (crz & crx) to decide which gates to apply
def step4(qc, qubit, crz, crx):
# Here we use c_if to control our gates with a classical
# bit instead of a qubit
qc.x(qubit).c_if(crx, 1) # Apply gates if the registers
qc.z(qubit).c_if(crz, 1) # are in the state '1''
Now build the end to end circuit
## SETUP
qr = QuantumRegister(3, name="q") # Protocol uses 3 qubits
crz = ClassicalRegister(1, name="crz") # and 2 classical registers
crx = ClassicalRegister(1, name="crx")
qc = QuantumCircuit(qr, crz, crx)
## STEP 0
# First, let's initialize Alice's q0
qc.append(init_state, [0])
qc.barrier()
## STEP 1
# Now begins the teleportation protocol
step1(qc, 1, 2)
qc.barrier()
## STEP 2
# Send q1 to Alice and q2 to Bob
step2(qc, 0, 1)
## STEP 3
# Alice then sends her classical bits to Bob
step3(qc, 0, 1)
## STEP 4
# Bob decodes qubits
step4(qc, 2, crz, crx)
# Display the circuit
qc.draw('mpl')
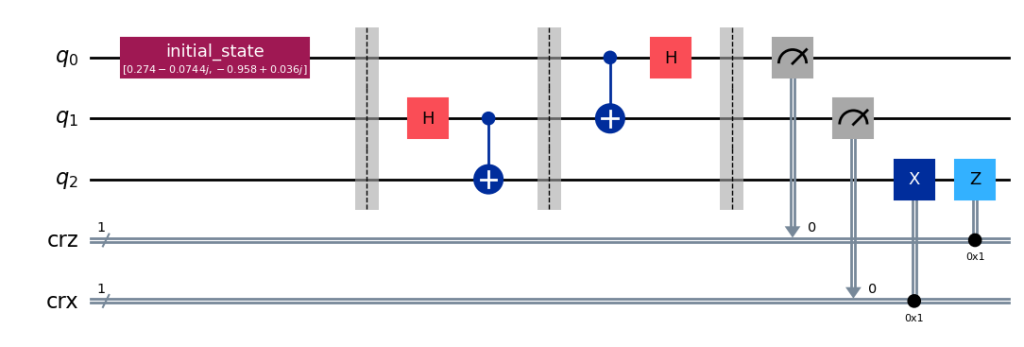
Lets execute the circuit on the simulator
# To get the eigenvector you should use the statevector simulator in the core of the circuit (without measurements)
backend = Aer.get_backend('statevector_simulator')
# Execute the circuit
job = backend.run(qc)
result_state = job.result()
outputstate = result_state.get_statevector(qc, decimals=3)
# Printing the state after X gate
print("\nQuantum state is:", outputstate)
# Plotting the Bloch Sphere
plot_bloch_multivector(outputstate)
Quantum state is: Statevector([ 0. +0.j , 0.274-0.074j, -0. +0.j , 0. +0.j ,
0. -0.j , -0.958+0.036j, -0. +0.j , -0. +0.j ],
dims=(2, 2, 2))
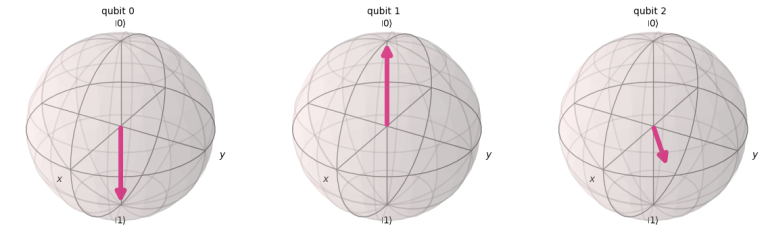
As we see the qubit 0 state has been transferred to qubit 2, and the qubit 0 state is lost.
Cheers!!
Amit Tomar