Model quantization is a technique used to optimize machine learning models by reducing their size and computational requirements, making them more efficient and suitable for deployment on resource-constrained devices such as smartphones, edge devices, and embedded systems.
Quantization involves converting the model’s parameters (weights and activations) from high-precision data types, such as 32-bit floating point (FP32), to lower-precision formats like 8-bit integers (INT8) or 16-bit floating point (FP16). This reduces the memory footprint and computational cost.
A model with 100 million weights and biases will occupy 400,000,000 bytes of storage if we store all the weights and biases as Float 32.
If we can convert the Float to Int 8, we will be able to store it in 1/4th of space.
The internals
A floating point number storage is explained by Fabien Sanglard https://fabiensanglard.net/floating_point_visually_explained/index.html
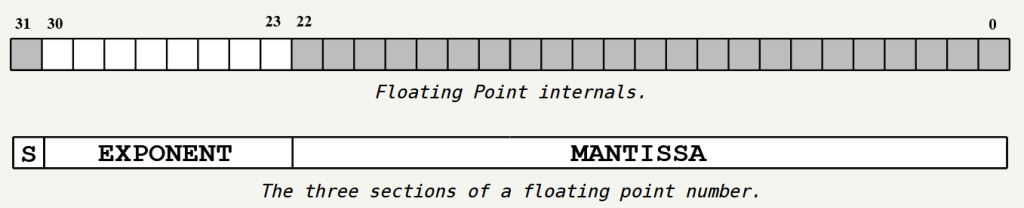
The first bit signifies if the number is positive or negative.
The EXPONENT/WINDOW uses 8 bits to store where a given number lies, is it between 2^0 and 2^1 or between 2^1 and 2^2 and so on upto 2^127 and 2^128.
This gives us the window which we have to partition to get our number. The MANTISSA/OFFSET is a 2^23 (8,388,608) size number which divides the WINDOW in 2^23 parts.
The value in the OFFSET signifies the location of the number in the window range above.
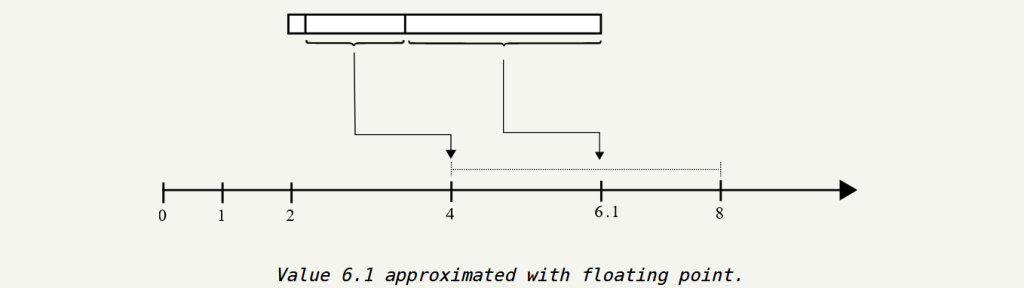
Lets say out number is in between 2^5 and 2^6, and the Offset is 0, so our number is going to be 2^5. but if the offset was 2^23, then then number would have been 2^6, and if the offset was in middle point 2^(22) then our number will be in the middle of 2^5 (32) and 2^6 (64) with a value of 48.
The following figure demonstrates how the number 6.1 is encoded. The window begins at 4 and extends to the next power of two, which is 8. The offset is positioned approximately halfway through the window. 2^23 X (6.1 – 4) / (8 – 4) = 4,404,019
How we quantize
The weights and biases generally lay in the range of -1 and 1.
We take this range and split it into 2^8 (256) parts, any number less than -1 gets assigned a value of -1 and any number more than 1 gets assigned a 1.
So a value of 0.75 will be stored as
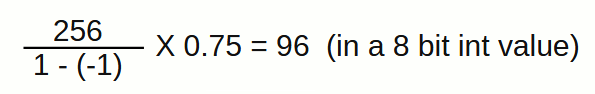
And a value of 0.43 will be stored as
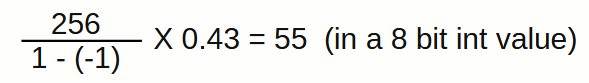
This storage also helps in performance of deployed model during the classification since the prediction algorithm has to work with ints (for multiplication and addition) rather than floats, and working with ints for these arithmetic operations ints are faster to operate on.
Types of Quantization
Post-Training Quantization:
Applied to a pre-trained model without additional training.
Simple and quick, but might result in slight accuracy degradation.
Quantization-Aware Training (QAT):
Involves simulating quantization effects during training to minimize accuracy loss.
More effective for preserving accuracy, especially for complex models.
Dynamic Quantization:
Quantizes weights and activations during runtime, adapting to input data dynamically.
Static Quantization:
Applies fixed quantization using calibration data to scale parameters effectively.
Example
Build a handwriting to digit classification model
# Load MNIST dataset
mnist = tf.keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Normalize the input image so that each pixel value is between 0 to 1.
train_images = train_images / 255.0
test_images = test_images / 255.0
# Define the model architecture.
model = keras.Sequential([
keras.layers.InputLayer(input_shape=(28, 28)),
keras.layers.Reshape(target_shape=(28, 28, 1)),
keras.layers.Conv2D(filters=12, kernel_size=(3, 3), activation='relu'),
keras.layers.MaxPooling2D(pool_size=(2, 2)),
keras.layers.Flatten(),
keras.layers.Dense(10)
])
# Train the digit classification model
model.compile(optimizer='adam',
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.fit(
train_images,
train_labels,
epochs=1,
validation_split=0.1,
)Apply quantization aware training to the whole model
import tensorflow_model_optimization as tfmot
quantize_model = tfmot.quantization.keras.quantize_model
# q_aware stands for for quantization aware.
q_aware_model = quantize_model(model)
# `quantize_model` requires a recompile.
q_aware_model.compile(optimizer='adam',
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
q_aware_model.fit(train_images, train_labels,
batch_size=500, epochs=1, validation_split=0.1)
q_aware_model.summary()Output
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
quantize_layer (QuantizeLa (None, 28, 28) 3
yer)
quant_reshape (QuantizeWra (None, 28, 28, 1) 1
pperV2)
quant_conv2d (QuantizeWrap (None, 26, 26, 12) 147
perV2)
quant_max_pooling2d (Quant (None, 13, 13, 12) 1
izeWrapperV2)
quant_flatten (QuantizeWra (None, 2028) 1
pperV2)
quant_dense (QuantizeWrapp (None, 10) 20295
erV2)
=================================================================
Total params: 20448 (79.88 KB)
Trainable params: 20410 (79.73 KB)
Non-trainable params: 38 (152.00 Byte)
_________________________________________________________________
Check the accuracy across models
_, baseline_model_accuracy = model.evaluate(
test_images, test_labels, verbose=0)
_, q_aware_model_accuracy = q_aware_model.evaluate(
test_images, test_labels, verbose=0)
print('Baseline test accuracy:', baseline_model_accuracy)
print('Quant test accuracy:', q_aware_model_accuracy)Output
Baseline test accuracy: 0.9550999999046326
Quant test accuracy: 0.9584000110626221In above case we see a better accuracy is being achieved, but important message here is that the impact on accuracy of the model by quantization is minimal.
Cheers!!!
Amit Tomar