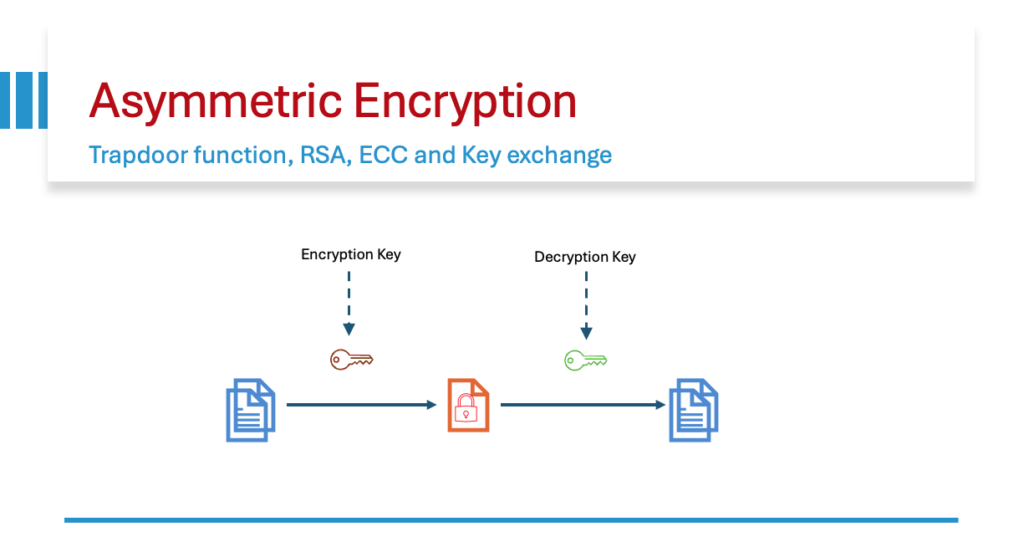
Public-key cryptography, or asymmetric cryptography, is the field of cryptographic systems that use pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic algorithms based on mathematical problems termed one-way/trap-door functions. Security of public-key cryptography depends on keeping the private key secret, the public key can be openly distributed without compromising security.
Trap door functions
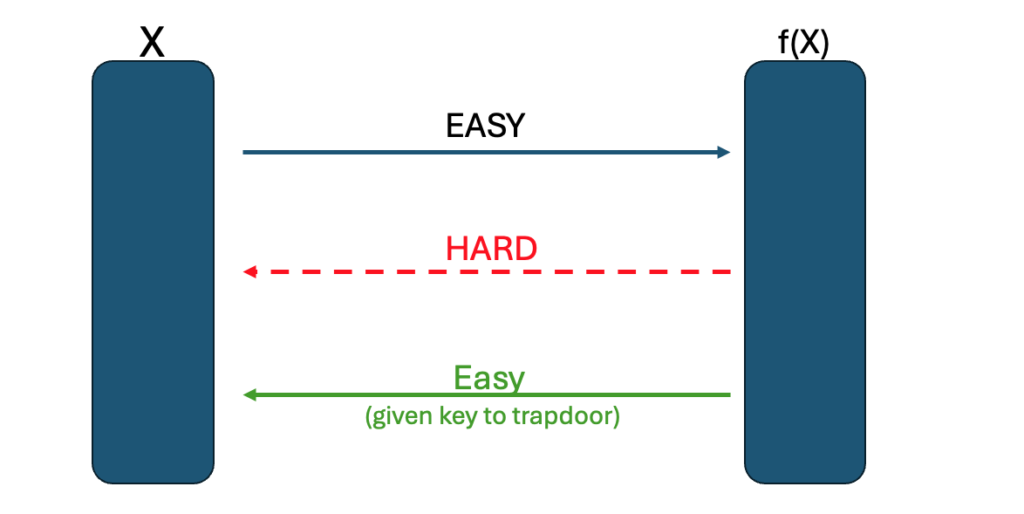
A one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, “easy” and “hard” are to be understood in the sense of computational complexity theory
Integer factorization problem
Given 2 prime numbers, it is easy to calculate the product of those 2 prime numbers. But given the product of 2 prime numbers, it is a exponential calculation to find the discreet prime numbers.
Given a general algorithm for integer factorization, any integer can be factored into its constituent prime factors by repeated application of this algorithm.
There are 2 considerations in this
Finding the prime number to use. In this case we have to come up with a 1024 / 2048 bit prime number first. Given a large number, we can find out if that number is prime or not is by using “Fermat’s little theorem”. The theorem states a^(P-1) mod P = 1. If this equations is satisfied for a given number a, it means P is prime. There is one minor catch here, if a and P are carmichael numbers (meaning greatest common divisor of a and P is 1) then the above prime number equation does not hold good, so this makes the theorem a probabilistic theorem. Which means that to decide if P is prime, we have to iterate it with couple of random values of a and then based on outputs we can decide if P is prime. There is also a Rabin-Miller algorithm which is efficient in finding large prime numbers.
Calculating prime factors is hard is just an assumption. It has not been proven that factorization problem is hard. General number field sieve can calculate prime factors fast, and someone may come up with a better one. With Quantum computers the prime factorization is very easy .
Discrete Logarithmic problem
This is based on congruent numbers which says
a mod m = b mod m then a and b are congruent.
57 mod 10 = 27 mod 10 so 57 and 27 are congruent numbers.
It is written as a ![]()
b (mod m)
Taking it to the next level, we want to use 3 numbers here to make it a trap door function
a ![]() b^c (mod m)
b^c (mod m)
meaning a mod m = b^c mod m.
In Private key cryptography, the a, b and m are exposed. but c is kept private. The a mod m can be calculated easily, but we have to make it hard to calculate the value of c.
For this we ensure b is a primitive root of m.
This means if we make m as a prime number, then m^1 mod m all the way to m^(m-1) mod m will yield all unique values from 1 to m-1 non-sequentially.
Now if a person knows a and m and calculate a mod m, and then tries to find a value of c where b^c mod m is same as a mod m, it is going to be a exponentially hard problem.
Exponentially hard problem
Why do we call it a problem to be a exponentially hard problem. You may say if I have to try all numbers upto a given number then it is a linear scale. But when we consider these equations, we use the number of bits as the guiding metric.
A 8 bit integer will go only up to 256, but a 16 bit integer will go upto 256*256 = 65536. So if we just double the bits the problem domain expands exponentially, and when we talk about prime numbers here we use 1024 or 2048 bit numbers.
RSA (Rivest–Shamir–Adleman)
The RSA algorithm involves four steps: key generation, key distribution, encryption, and decryption.
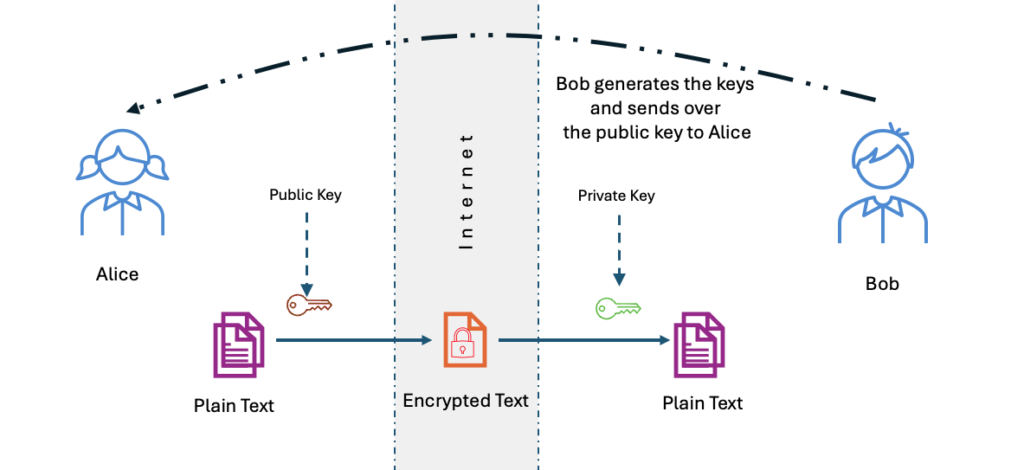
There are 3 numbers involved here. P and Q are 2 prime numbers, and N is P X Q
We have to find the Euler’s Phi value for N which states that if a number is a prime number then it will have (n-1) relative primes.
2 numbers are relative prime to each other if gcd(a,b) = 1. And if N = PxQ then Euler’s totient function derives the value of Phi(N) = (P-1)x(Q-1)
The algorithm
-
- Take 2 prime numbers p and q
-
- Get
n = p * qand get the Euler’s phi asPhi(n) = (p-1)x(q-1)
- Get
-
- Find a number e(encrypter) (using random generations) so
gcd (e, Phi(n)) = 1. Meaning e and O(n) are relative primes.
- Find a number e(encrypter) (using random generations) so
-
- Find a number d (decrypter) (also called modular inverse of e) so
d * e mod Phi(n) = 1
- Find a number d (decrypter) (also called modular inverse of e) so
Our public key is (e,n) and private key is (d,n)
To use the keys we use the following formula
cipherText = plainText ^ e mod n
plainText = cipherText ^ d mod nTo find e at step 3 above we can use Euclidean Algorithm to calculate GCD without calculating factors of both numbers
GCD (84 , 36)
84 = 36q + r -> 84 = 362 + 12
GCD (36,12)
36 = 12q + r -> 36 = 123 + 0Since remainder is 0, so 12 is selected as GCD
Alternatively we can simply use BigInteger.gcd method
So we generate a random e and see if gcd (e, Phi(n)) = 1 otherwise try again with a new value of e
To calculate e in Step 4 we need Extended Euclidean algorithm
ax+by= gcd(a,b)So we have to find correct values of x and y
36 x + 86 y = gcd (36,86)
86 = 36(2) + 14 >>> 86 - 36(2) = 14
36 = 14(2) + 8 >>> 36 - 14(2) = 8
14 = 8(1) + 6 >>> 14 - 8(1) = 6
8 = 6(1) + 2 >>> 8 - 6(1) = 2
6 = 2(3) + 0Now going back in reverse and substituting till we get all 36s and 86s
8 - 6 = 2
8 - [14 - 8] = 2
36 - 14(2) - [14 - (36 - 14(2))] = 2
36 - ((86 - 36(2)2) - [(86 - 36(2)) - 36 + (86 - 36(2))(2)] = 2
36 - 86*2 + 36*4 - [86 - 36*2 - 36 + 86*2 - 36*4] = 2
36 - 86*2 + 36*4 - 86 + 36*2 + 36 - 86*2 + 36*4 = 2
36(12) + 86(-5) = 2So x is 12 and y is -5
Now x is modular multiplicative inverse of a mod b and y is the modular multiplicative inverse of b mod a
since for us we were trying to find mod inverse of e mod 0(n) and our inputs were e and O(n) so we have to pick x since e was mapped to a.
Putting it together (You can use a implementation from Bouncy castle as well)
private SecureRandom random = new SecureRandom();
// p and q prime numbers
BigInteger p = BigInteger.probablePrime(1024, random);
BigInteger q = BigInteger.probablePrime(1024, random);
// n=q*p
n = p.multiply(q);
// Euler's totient phi function (p-1)*(q-1)
BigInteger phi = (p.subtract(BigInteger.ONE)).multiply(q.subtract(BigInteger.ONE));
// e so that gcd(phi,e)=1
BigInteger e = new BigInteger(1024, random);
while(!e.gcd(phi).equals(BigInteger.ONE)) {
e = new BigInteger(phi.bitLength(), random);
}
// find d which is modular inverse of e mod phi (Extended Euclidean algorithm)
BigInteger d = e.modInverse(phi);
BigInteger privateKey = d;
BigInteger publicKey = e;
String message = "This is a message";
//Encrypt the message using public key
byte[] messageByte = message.getBytes();
BigInteger messageIntE = new BigInteger(messageByte);
// cipher text = message ^ e mod n
String cipherText = messageIntE.modPow(e, n);
//Decrypt the message using private key
BigInteger messageIntD = cipherText.modPow(d, n);
String plainText = new String(messageIntD.toByteArray());Elliptic-curve cryptography (ECC)
An elliptic curve is a plane curve over a finite field which consists of the points satisfying the equation
y^{2} = x^{3} + ax + b
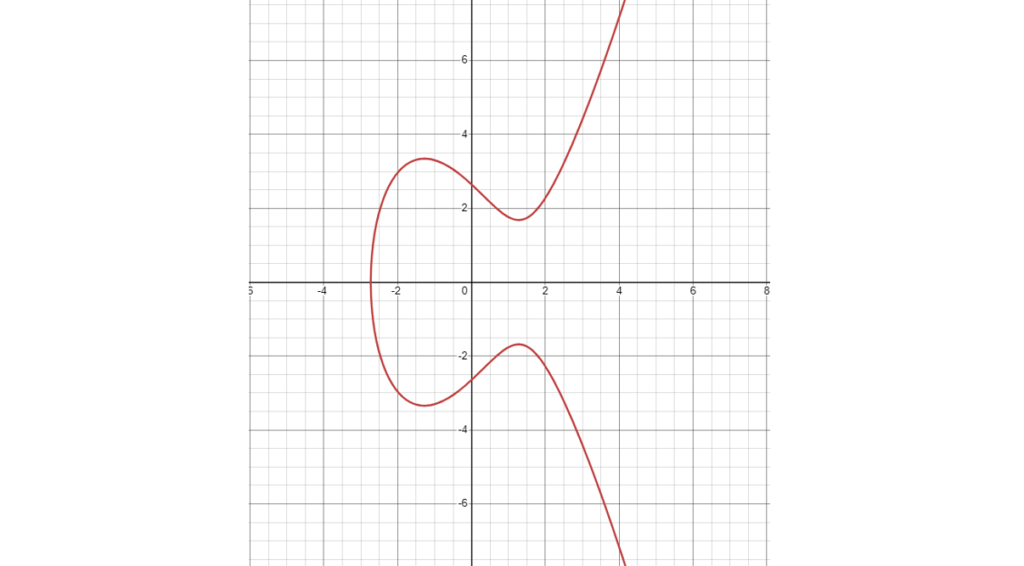
So all points lying on the curve will satisfy the above equation.
The trap door function
In ECC we use point addition as a trap door function
If we know we have to get the value of P(x1,y1) = n*P(x0,y0) when n and P(x0,y0) are known then it can be simply calculated with the point addition and doubling algorithm below.
But if we know P(x0,y0) and P(x1,y1) and we have to find the value of n, then the only solution for it is to add it over and over again which is a exponentially large problem.
Point addition
Now a line across the curve will intersect with the curve at 3 points.
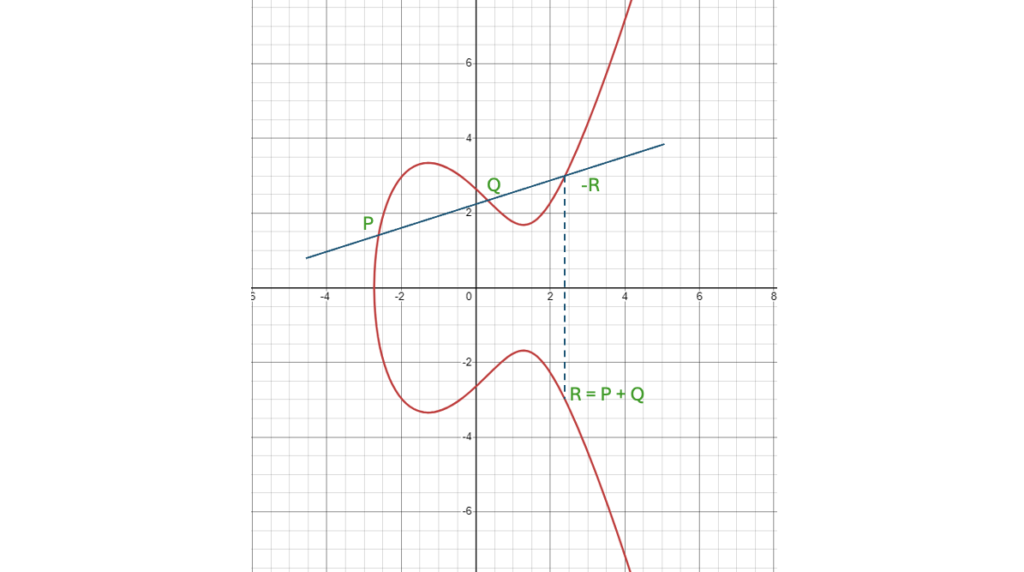
P(x1, y1) + Q(x2, y2) = R(x3,y3)The line which goes through P and Q will intersect the curve at a reflection point of R namely -R(x3,-y3)
How to find x3,y3
Any straight line can be defined as y = mx + d
if we define the slope as
m = (y2-y1)/(x2-x1)// if we have 2 pointsm = (3*x^{2} + a)/ 2y// if we have P1 = P2 we need to use differential equation
Then x3 and y3 can be derived as
x3 = m^{2} -x1 -x2
y3 = m * (x1 - x3) - y1So now we know how to add one point to another or double a point
Using this we can get a answer to n * P using below table
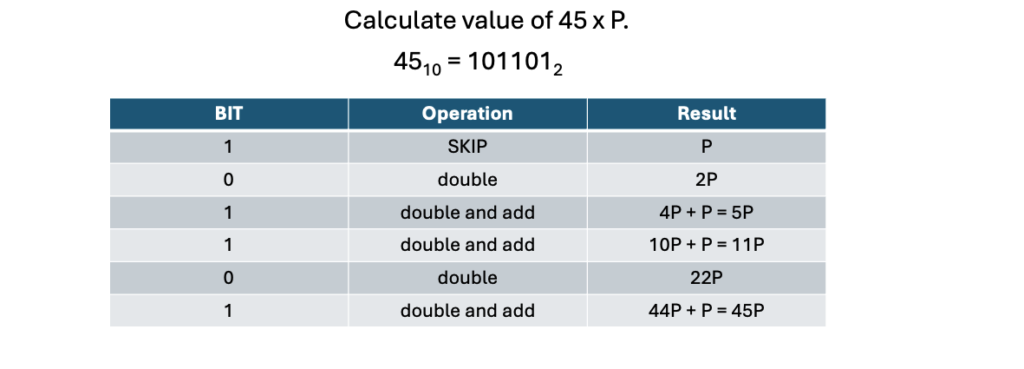
So instead of adding P to itself 45 times, we were able to get 45P in a couple of steps.
Key Exchange using ECC
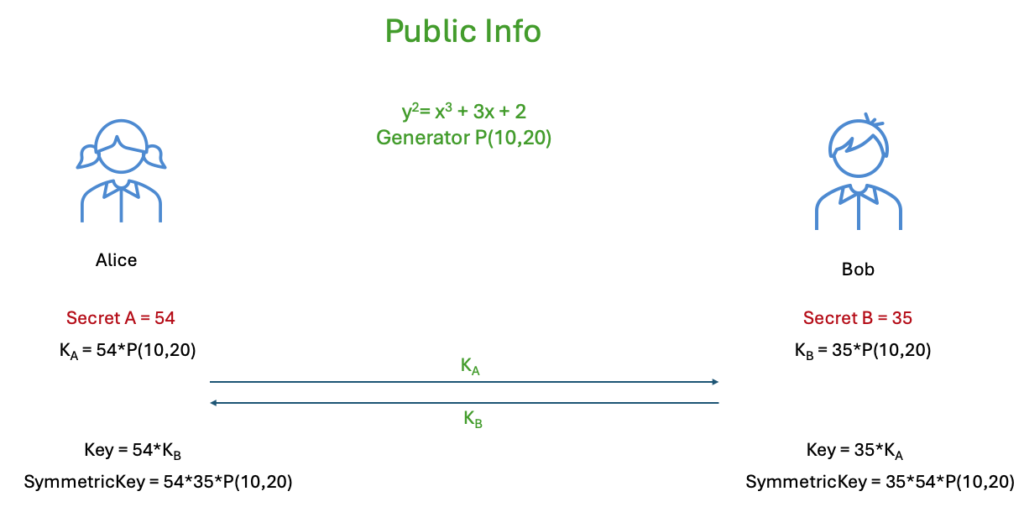
Lets say we have a ECC curve with a = 3 and b = 2
We start with a Generator point P (10,20)
Assuming Alice generates a private number A=54, She generates Key(a) = 54P
Now Bob generates another private number B = 35, He generates Key(b) = 35P
Alice sends K(a) to Bob, and Bob sends K(b) to Alice.
So at this time a, b, P(10,20) and K(a) and K(b) are all known to public. Only A and B are secret.
Alice will use Key(b) to calculate AK(b) which is 54K(b) which is 54*35*P
Bob will use Key(a) to calculate BK(a) which is 35K(a) which is 35*54*P
This key exchange method is called Diffie–Hellman key exchange
This results in Alice and Bob having the same Symmetric Private Key which they can use to encrypt and decrypt.
Cheers – Amit Tomar